Acasă
Hazna
Ecuația cercului pe planul de coordonate. Coordonatele carteziene ale punctelor plane

Ecuația cercului pe planul de coordonate. Coordonatele carteziene ale punctelor plane

Definiția 1 . Axa numerica ( linie numerică, linie de coordonate) Ox se numește dreptă pe care se alege punctul O punct de referință (originea coordonatelor)(fig.1), direcție

O → X

enumerate ca direcție pozitivăși se marchează un segment, a cărui lungime este luată ca unitate de lungime.

Definiția 2 . Segmentul, a cărui lungime este luată ca unitate de lungime, se numește scară.

Fiecare punct al axei numerice are o coordonată, care este un număr real. Coordonata punctului O este egală cu zero. Coordonata unui punct arbitrar A situat pe raza Ox este egală cu lungimea segmentului OA . Coordonata unui punct arbitrar A al axei numerice, care nu se află pe raza Ox , este negativă, iar în valoare absolută este egală cu lungimea segmentului OA .

Definiția 3 . Sistemul de coordonate carteziene dreptunghiulare Oxy pe plan sunați pe cei doi reciproc perpendicular axele numerice Ox si Oy cu aceeasi scarași origine comunăîn punctul O, în plus, astfel încât rotația de la raza Ox printr-un unghi de 90 ° față de raza Oy se efectuează în direcția în sens invers acelor de ceasornic(Fig. 2).

Observație . Sistemul de coordonate carteziene dreptunghiulare Oxy prezentat în figura 2 se numește sistemul de coordonate corect, Spre deosebire de sisteme de coordonate stânga, în care rotirea fasciculului Ox la un unghi de 90° față de fasciculul Oy se realizează în sensul acelor de ceasornic. În acest ghid, noi luați în considerare numai sistemele de coordonate corecte fără să o menționăm în mod special.

Dacă introducem un sistem de coordonate carteziene dreptunghiulare Oxy pe plan, atunci fiecare punct al planului va dobândi două coordonate – abscisăși ordonată, care se calculează după cum urmează. Fie A un punct arbitrar al planului. Să lăsăm perpendicularele din punctul A AA 1 și AA 2 la liniile Ox și, respectiv, Oy (Fig. 3).

Definiția 4 . Abscisa punctului A este coordonata punctului A 1 pe axa numerică Ox, ordonata punctului A este coordonata punctului A 2 pe axa numerică Oy .

Denumirea . Coordonatele (abscisa si ordonata) ale unui punct A în sistemul de coordonate carteziene dreptunghiulare Oxy (Fig. 4) este de obicei notat A(X;y) sau A = (X; y).

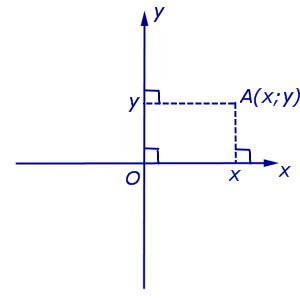
Observație . Punctul O, numit origine, are coordonate O(0 ; 0) .

Definiția 5 . În sistemul de coordonate carteziene dreptunghiulare Oxy, axa numerică Ox se numește axa absciselor, iar axa numerică Oy se numește axa ordonatelor (Fig. 5).

Definiția 6 . Fiecare sistem de coordonate carteziene dreptunghiulare împarte planul în 4 sferturi ( cadrane), a căror numerotare este prezentată în Figura 5.

Definiția 7 . Se numește un plan pe care este dat un sistem de coordonate carteziene dreptunghiulare plan de coordonate.

Observație . Axa absciselor este dată pe planul de coordonate de ecuație y= 0 , axa y este dată pe planul de coordonate de ecuație X = 0.

Afirmația 1 . Distanța dintre două puncte plan de coordonate

A 1 (X 1 ;y 1) și A 2 (X 2 ;y 2)

calculat conform formulei

Dovada . Luați în considerare figura 6.

Fie ca cercul să aibă o rază , iar centrul său este în punct
. Punct
se află pe cerc dacă și numai dacă modulul vectorului
egală , acesta este. Ultima egalitate este valabilă dacă și numai dacă

Ecuația (1) este ecuația cercului dorită.

Ecuația unei drepte care trece printr-un punct dat este perpendiculară pe un vector dat


perpendicular pe vector
.

Punct

și
sunt perpendiculare. Vectori
și
sunt perpendiculare dacă și numai dacă produsul lor punctual este zero, adică
. Folosind formula de calcul a produsului scalar al vectorilor dat de coordonatele lor, scriem ecuația dreptei dorite sub forma

Luați în considerare un exemplu. Aflați ecuația unei drepte care trece prin

mijlocul segmentului AB este perpendicular pe acest segment dacă coordonatele punctelor sunt, respectiv, egale cu A (1; 6), B (5; 4).

Vom argumenta după cum urmează. Pentru a găsi ecuația unei drepte, trebuie să cunoaștem punctul prin care trece această dreaptă și vectorul perpendicular pe această dreaptă. Vectorul perpendicular pe această dreaptă va fi vectorul, deoarece, după condiția problemei, dreapta este perpendiculară pe segmentul AB. punct
determinăm din condiția ca dreapta să treacă prin mijlocul lui AB. Avem . În acest fel
iar ecuația va lua forma.

Să clarificăm întrebarea dacă această dreaptă trece prin punctul M(7;3).

Avem , ceea ce înseamnă că această linie nu trece prin punctul specificat.

Ecuația unei drepte care trece printr-un punct dat, paralelă cu un vector dat

Lasă linia să treacă prin punct
paralel cu vectorul
.

Punct
se află pe o linie dacă și numai dacă vectorii
și
coliniare. Vectori
și
sunt coliniare dacă și numai dacă coordonatele lor sunt proporționale, adică

(3)

Ecuația rezultată este ecuația dreptei dorite.

Ecuația (3) poate fi reprezentată ca

, Unde ia orice valoare
.

Prin urmare, putem scrie

, Unde
(4)

Sistemul de ecuații (4) se numește ecuații parametrice ale dreptei.

Luați în considerare un exemplu. Aflați ecuația unei drepte care trece prin puncte. Putem construi ecuația unei drepte dacă cunoaștem un punct și un vector paralel sau perpendicular pe acesta. Sunt două puncte disponibile. Dar dacă două puncte se află pe o dreaptă, atunci vectorul care le conectează va fi paralel cu această dreaptă. Prin urmare, folosim ecuația (3), luând ca vector
vector
. Primim

(5)

Ecuația (5) se numește ecuația unei drepte care trece prin două puncte date.

Ecuația generală a unei drepte

Definiție. Ecuația generală a unei drepte de ordinul întâi pe un plan este o ecuație de formă
, Unde
.

Teorema. Orice linie dreaptă din plan poate fi dată ca o ecuație de linie de ordinul întâi, iar orice ecuație de linie de ordinul întâi este o ecuație a unei linii drepte din plan.

Prima parte a acestei teoreme este ușor de demonstrat. Pe orice linie, puteți specifica un punct
vector perpendicular pe acesta
. Atunci, conform (2), ecuația unei astfel de drepte are forma Denota
. Apoi ecuația va lua forma
.

Acum să trecem la a doua parte a teoremei. Să existe o ecuație
, Unde
. Pentru certitudine, vom presupune
.

Să rescriem ecuația sub forma:

;

Luați în considerare un punct din avion
, Unde
. Atunci ecuația rezultată are forma și este ecuația unei drepte care trece prin punctul
perpendicular pe vector
. Teorema a fost demonstrată.

În procesul de demonstrare a teoremei, am demonstrat pe parcurs

Afirmație. Dacă există o ecuație în linie dreaptă
, apoi vectorul
perpendicular pe această dreaptă.

Tip ecuație
se numește ecuația generală a unei drepte într-un plan.

Să fie o linie
și punct
. Este necesar să se determine distanța de la punctul specificat la linie.

Luați în considerare un punct arbitrar
pe o linie dreaptă. Avem
. Distanţă din punct de vedere
la linia dreaptă este egală cu modulul proiecției vectorului
pe vector
perpendicular pe această dreaptă. Avem

,

transformare, obținem formula:

Fie două drepte date de ecuațiile generale

,
. Apoi vectorii

perpendicular pe prima și, respectiv, pe a doua linie. Colţ
dintre linii este egal cu unghiul dintre vectori
,
.

Atunci formula pentru determinarea unghiului dintre linii este:

.

Condiția de perpendicularitate a dreptelor are forma:

.

Liniile sunt paralele sau coincid dacă și numai dacă vectorii

coliniare. în care condiţia coincidenţei liniilor are forma:
,

iar condiția fără intersecție este scrisă astfel:
. Demonstrați singur ultimele două condiții.

Să investigăm comportamentul dreptei conform ecuației sale generale.

Să fie dată ecuația generală a unei drepte
. În cazul în care un
, apoi linia trece prin origine.

Luați în considerare cazul în care niciunul dintre coeficienți nu este egal cu zero
. Rescriem ecuația sub forma:

,

,

Unde
. Aflați semnificația parametrilor
. Aflați punctele de intersecție ale dreptei cu axele de coordonate. La
avem
, și atunci când
avem
. Acesta este
- acestea sunt segmentele care sunt tăiate printr-o linie dreaptă pe axele de coordonate. Prin urmare, ecuația
se numește ecuația unei drepte în segmente.

Când
avem

. Când
avem
. Adică, linia va fi paralelă cu axa .

Amintește-ți asta panta unei drepte se numește tangenta unghiului de înclinare a acestei linii la axă
. Lăsați linia dreaptă tăiată pe axă segment de linie și are o pantă . Lasă punctul
se află pe asta

Apoi
==. Și ecuația unei linii drepte se va scrie sub formă

.

Lasă linia să treacă prin punct
și are o pantă . Lasă punctul
se află pe această linie.

Apoi =
.

Ecuația rezultată se numește ecuația unei drepte care trece printr-un punct dat cu o pantă dată.

Să fie date două linii
,
. Denota
este unghiul dintre ele. Lăsa ,unghiuri de înclinare față de axa X a liniilor corespunzătoare

Apoi
=
,
.

Atunci condiția dreptelor paralele are forma
, și condiția de perpendicularitate

În concluzie, luăm în considerare două probleme.

O sarcină . Vârfurile triunghiului ABC au coordonatele: A(4;2), B(10;10), C(20;14).

Aflați: a) ecuația și lungimea medianei trase din vârful A;

b) ecuația și lungimea înălțimii trase din vârful A;

c) ecuaţia bisectoarei trasă din vârful A;

Să definim ecuația mediei AM.

Punctul M () este mijlocul segmentului BC.

Apoi , . Prin urmare, punctul M are coordonatele M(15;17). Ecuația mediană în limbajul geometriei analitice este ecuația unei drepte care trece prin punctul A (4; 2) paralel cu vectorul = (11; 15). Atunci ecuația mediană este Lungimea mediană AM= .

Ecuația înălțimii AS este ecuația unei drepte care trece prin punctul A(4;2) perpendicular pe vectorul =(10;4). Atunci ecuația înălțimii este 10(x-4)+4(y-2)=0, 5x+2y-24=0.

Lungimea înălțimii este distanța de la punctul A (4; 2) la linia dreaptă BC. Această dreaptă trece prin punctul B(10;10) paralel cu vectorul =(10;4). Ecuația sa este , 2x-5y+30=0. Distanța AS de la punctul A(4;2) la dreapta BC este, prin urmare, egală cu AS= .

Pentru a determina ecuația bisectoarei, găsim un vector paralel cu această dreaptă. Pentru a face acest lucru, folosim proprietatea diagonalei unui romb. Dacă vectorii unitari sunt puși deoparte de punctul A și sunt direcționați în mod egal cu vectorii, atunci un vector egal cu suma lor va fi paralel cu bisectoarea. Atunci avem =+.

={6;8}, , ={16,12}, .

Apoi = Vectorul = (1; 1), coliniar cu cel dat, poate servi ca vector de direcție al dreptei dorite. Atunci ecuația dreptei dorite a văzut x-y-2=0.

O sarcină. Râul curge în linie dreaptă trecând prin punctele A(4;3) și B(20;11). Scufița Roșie locuiește în punctul C(4;8), iar bunica ei locuiește în punctul D(13;20). În fiecare dimineață, Scufița Roșie ia o găleată goală din casă, merge la râu, trage apă și i-o duce bunicii. Găsiți cea mai scurtă cale pentru Scufița Roșie.

Să găsim punctul E, simetric față de bunica, relativ la râu.

Pentru a face acest lucru, găsim mai întâi ecuația dreptei de-a lungul căreia curge râul. Această ecuație poate fi considerată drept ecuația unei drepte care trece prin punctul A(4;3) paralel cu vectorul. Atunci ecuația dreptei AB are forma.

În continuare, găsim ecuația dreptei DE care trece prin punctul D perpendicular pe AB. Poate fi considerată ca ecuația unei drepte care trece prin punctul D, perpendicular pe vector
. Avem

Acum să găsim punctul S - proiecția punctului D pe dreapta AB, ca intersecția dreptelor AB și DE. Avem un sistem de ecuații

.

Prin urmare, punctul S are coordonatele S(18;10).

Deoarece S este punctul de mijloc al segmentului DE, atunci .

De asemenea.

Prin urmare, punctul E are coordonatele E(23;0).

Să găsim ecuația dreptei CE, cunoscând coordonatele a două puncte ale acestei drepte

Găsim punctul M ca intersecția dreptelor AB și CE.

Avem un sistem de ecuații

.

Prin urmare, punctul M are coordonate
.

Subiectul 2 Conceptul de ecuație de suprafață în spațiu. Ecuația sferei. Ecuația unui plan care trece printr-un punct dat este perpendiculară pe un vector dat. Ecuația generală a planului și studiul lui Condiția de paralelism a două plane. Distanța de la un punct la un plan. Conceptul de ecuație a dreptei. Linie dreaptă în spațiu. Ecuații canonice și parametrice ale unei drepte în spațiu. Ecuațiile unei drepte care trece prin două puncte date. Condiții de paralelism și perpendicularitate a unei drepte și a unui plan.

Mai întâi, să definim conceptul de ecuație de suprafață în spațiu.

Lasă în spațiu
se da o anumita suprafata . Ecuația
se numește ecuația suprafeței daca sunt indeplinite doua conditii:

1.pentru orice punct
cu coordonate
culcat la suprafata,
, adică coordonatele sale satisfac ecuația suprafeței;

2. orice punct
, ale cărui coordonate satisfac ecuația
, se află pe linie.


Geometria analitică oferă metode uniforme pentru rezolvarea problemelor geometrice. Pentru a face acest lucru, toate punctele și liniile date și dorite sunt raportate la același sistem de coordonate.

Într-un sistem de coordonate, fiecare punct poate fi caracterizat prin coordonatele sale, iar fiecare linie printr-o ecuație cu două necunoscute, din care această linie este un grafic. Astfel, problema geometrică se reduce la una algebrică, unde toate metodele de calcul sunt bine dezvoltate.

Un cerc este un loc de puncte cu o proprietate specifică (fiecare punct al cercului este echidistant de un punct, numit centru). Ecuația cercului trebuie să reflecte această proprietate, să satisfacă această condiție.

Interpretarea geometrică a ecuației unui cerc este linia unui cerc.

Dacă plasăm un cerc într-un sistem de coordonate, atunci toate punctele cercului îndeplinesc o condiție - distanța de la ele la centrul cercului trebuie să fie aceeași și egală cu cercul.

Cerc centrat într-un punct DAR si raza R plasat în planul de coordonate.

Dacă coordonatele centrului (a;b) , și coordonatele oricărui punct de pe cerc (X y) , atunci ecuația cercului are forma:


Dacă pătratul razei unui cerc este egal cu suma diferențelor pătrate ale coordonatelor corespunzătoare ale oricărui punct de pe cerc și centrul acestuia, atunci această ecuație este ecuația unui cerc dintr-un sistem de coordonate plan.

Dacă centrul cercului coincide cu punctul de origine, atunci pătratul razei cercului este egal cu suma pătratelor coordonatelor oricărui punct de pe cerc. În acest caz, ecuația cercului ia forma:



Prin urmare, orice figură geometrică ca loc de puncte este determinată de o ecuație care raportează coordonatele punctelor sale. În schimb, ecuația care raportează coordonatele X și la , definiți o dreaptă ca loc al punctelor din planul ale cărui coordonate satisfac ecuația dată.

Exemple de rezolvare a problemelor despre ecuația unui cerc

O sarcină. Scrieți o ecuație pentru un cerc dat

Scrieți o ecuație pentru un cerc centrat în punctul O (2;-3) și cu raza 4.

Soluţie.
Să ne întoarcem la formula ecuației cercului:
R 2 \u003d (x-a) 2 + (y-b) 2

Înlocuiți valorile în formulă.
Raza cercului R = 4
Coordonatele centrului cercului (în funcție de condiție)
a = 2
b=-3

Primim:
(x - 2 ) 2 + (y - (-3 )) 2 = 4 2
sau
(x - 2 ) 2 + (y + 3 ) 2 = 16 .

O sarcină. Un punct aparține ecuației unui cerc

Verificați dacă punctul aparține A(2;3) ecuația cercului (x - 2) 2 + (y + 3) 2 = 16 .

Soluţie.
Dacă un punct aparține unui cerc, atunci coordonatele acestuia satisfac ecuația cercului.
Pentru a verifica dacă un punct cu coordonate date aparține cercului, înlocuim coordonatele punctului în ecuația cercului dat.

În ecuația ( X - 2) 2 + (y + 3) 2 = 16
substituim, dupa conditie, coordonatele punctului A (2; 3), adica
x=2
y=3

Să verificăm adevărul egalității obținute
(X - 2) 2 + (y + 3) 2 = 16
(2 - 2) 2 + (3 + 3) 2 = 16
0 + 36 = 16 egalitatea este greșită

Deci punctul dat nu apartin ecuația cerc dată.

Dacă plasați un cerc cu număr de unitate pe planul de coordonate, atunci puteți găsi coordonatele punctelor sale. Cercul numeric este poziționat astfel încât centrul său să coincidă cu originea planului, adică punctul O (0; 0).

De obicei, pe un cerc cu număr de unitate, punctele sunt marcate corespunzător originii pe cerc

  • sferturi - 0 sau 2π, π/2, π, (2π)/3,
  • sferturi din mijloc - π/4, (3π)/4, (5π)/4, (7π)/4,
  • al treilea trimestru - π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.

Pe planul de coordonate, cu aranjamentul de mai sus a cercului unitar pe acesta, se pot găsi coordonatele corespunzătoare acestor puncte ale cercului.

Este foarte ușor să găsești coordonatele capetelor de sferturi. În punctul 0 al cercului, coordonata x este 1, iar y este 0. Putem scrie A (0) = A (1; 0).

Sfârșitul primului trimestru va fi situat pe axa y pozitivă. Prin urmare, B (π/2) = B (0; 1).

Sfârșitul celui de-al doilea trimestru este pe abscisa negativă: C (π) = C (-1; 0).

Sfârșitul celui de-al treilea trimestru: D ((2π)/3) = D (0; -1).

Dar cum să găsiți coordonatele punctelor medii ale sferturii? Pentru a face acest lucru, construiți un triunghi dreptunghic. Ipotenuza sa este un segment de la centrul cercului (sau originea) până la mijlocul sfertului de cerc. Aceasta este raza cercului. Deoarece cercul este unitate, ipotenuza este egală cu 1. Apoi, se trasează o perpendiculară dintr-un punct al cercului pe orice axă. Lasă-l pe axa x. Rezultă un triunghi dreptunghic, ale cărui lungimi ale catetelor sunt coordonatele x și y ale punctului cercului.

Un sfert de cerc are 90º. Și jumătate de sfert este 45º. Deoarece ipotenuza este trasă în punctul din mijlocul sfertului, unghiul dintre ipotenuză și catetul care iese din origine este de 45º. Dar suma unghiurilor oricărui triunghi este 180º. Prin urmare, unghiul dintre ipotenuză și celălalt catete rămâne și el 45º. Se dovedește un triunghi dreptunghic isoscel.

Din teorema lui Pitagora obținem ecuația x 2 + y 2 = 1 2 . Deoarece x = y și 1 2 = 1, ecuația se simplifică la x 2 + x 2 = 1. Rezolvând-o, obținem x = √1 = 1/√2 = √2/2.

Astfel, coordonatele punctului M 1 (π/4) = M 1 (√2/2; √2/2).

În coordonatele punctelor punctelor mijlocii ale altor sferturi, doar semnele se vor schimba, iar modulele de valori vor rămâne aceleași, deoarece triunghiul dreptunghic se va întoarce doar. Primim:
M2 ((3π)/4) = M2 (-√2/2; √2/2)
M3 ((5π)/4) = M3 (-√2/2; -√2/2)
M4 ((7π)/4) = M4 (√2/2; -√2/2)

Atunci când se determină coordonatele celor trei părți ale sferturilor de cerc, se construiește și un triunghi dreptunghic. Dacă luăm punctul π/6 și desenăm o perpendiculară pe axa x, atunci unghiul dintre ipotenuză și cateta situată pe axa x va fi de 30º. Se știe că piciorul situat opus unui unghi de 30º este egal cu jumătate din ipotenuză. Deci am găsit coordonata y, este egală cu ½.

Cunoscând lungimile ipotenuzei și ale unuia dintre catete, după teorema lui Pitagora găsim celălalt catete:
x 2 + (½) 2 = 1 2
x 2 \u003d 1 - ¼ \u003d ¾
x = √3/2

Astfel T 1 (π/6) = T 1 (√3/2; ½).

Pentru punctul din a doua treime a primului trimestru (π / 3), este mai bine să desenați o perpendiculară pe axa pe axa y. Apoi unghiul de la origine va fi, de asemenea, de 30º. Aici, coordonata x va fi deja egală cu ½, respectiv y, √3/2: T 2 (π/3) = T 2 (½; √3/2).

Pentru alte puncte din al treilea trimestru, semnele și ordinea valorilor coordonatelor se vor schimba. Toate punctele care sunt mai aproape de axa x vor avea o valoare modulo a coordonatei x egală cu √3/2. Acele puncte care sunt mai aproape de axa y vor avea o valoare modulo y egală cu √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T4 ((5π)/6) = T4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T8 ((11π)/6) = T8 (√3/2; -½)



Secțiuni